Differential Equations : Methods for obtaining numerical and analytic solutions of elementary differential equations. Applications are also discussed with an emphasis on modeling.
Topics covered include methods for obtaining numerical and analytic solutions of elementary differential equations. Applications are also discussed with an emphasis on modelling. Topic outline:
- First Order Differential equations
- Systems of two first order equations
- Second order linear equations
- Modelling real-life situations
- Laplace Transform Methods
- Nonlinear Differential Equations and Stability
- Numerical approximation of solutions by Euler’s method
The learning outcome for this course includes the following.
- Classify differential equations (by order, linearity, homogeneity, exact, separable, etc) and apply their classification to determine which methods can be used to solve them.
- Solve differential equations using techniques introduced throughout this course and interpret the solution to characterize a system.
- Model real-life situations using differential equations.
- Analyze mathematical statements and solutions of differential equations visually (for example, by using a direction field or a phase portrait).
Write logical progressions of precise mathematical statements to justify and communicate your reasoning.
We will need to do a lot of calculus (differentiation and integration) and linear algebra (solving linear systems and computing eigenvalues and eigenvectors).
Differential Equations: An Introduction to Modern Methods & Applications, 3rd edition, by Brannan & Boyce. Wiley. ISBN 9781118531778.
Purchase of the textbook is not necessary. Slides with complete lessons will be posted on Canvas.
HOMEWORK : Weekly Homework will be assigned on Webwork due every Tuesday 11:59pm. You are expected to understand all the homework problems for all the tests. No late submission is allowed. Instead, Two lowest HW scores will be dropped.
QUIZZES: There will be five quizzes of 20 minutes during Studio on Thursdays. Tentative dates are Aug 28, Sep 11, Oct 9, Oct 23 and Nov 27. One lowest quiz score will be dropped.
MIDTERMS: There will be two midterms of 1h 15 minutes during Lecture on Wednesday. Tentative dates are Sep 24 and Nov 12. There’s no dropping for midterm.
FINAL EXAM: The final exam will cover all course materials and will be administered during the final exam period (the exact date will be announced later.) for 2 hours and 50 minutes. All students must take the final examination. The final exam schedule is non-negotiable. No earlier or late final exam is allowed due to travel plans.
Grades
Final grades will be calculated using whichever of the following weights yields the higher grade.
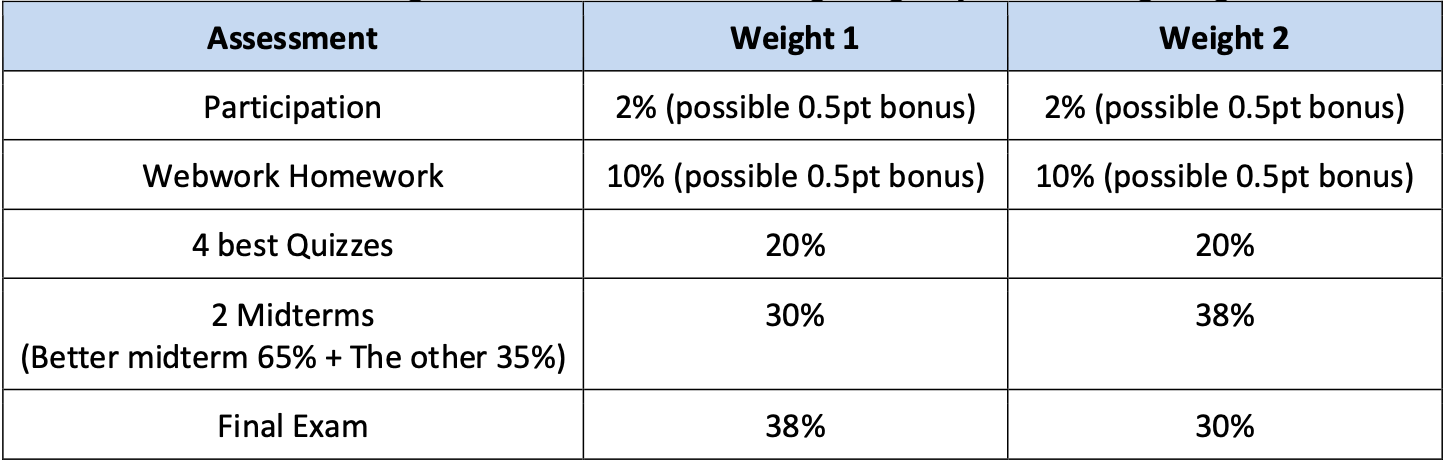
CIOS Bonus: When the participation to the survey for both Lecture and Studio is above 85%, there will be 1pt bonus awarded to the entire class. (Total 2 points, out of 100, bonus in the final grade is possible.)
A midterm grade will be assigned around September 30. A satisfactory grade will be assigned to all students with a midterm average of 70% or higher.
Letter grades will be determined based on the usual intervals. A: 90% and higher, B: [80%, 90%), C: [70%, 80%), D: [60%, 70%), F: [0%, 60%). For example, a final grade of 89.99% is converted into a B, a final grade of 79.99% is converted into a C, and so on. There will be NO changes to these intervals because there will be an appropriate curve or make-up test depending on the average for each test. No individual curve, extra credits, or make-up exam (except for justified absences.)
PARTICIPATION: Attending class is important. Class attendance and participation for both lectures and studios will be recorded and scored on a 0-2.5 scale. The scale is determined as follows: 2.5 points for above 90% attendance for both Lecture and Studio, 2 points for above 80% attendance for both Lecture and Studio, and 1 point for above 80% in one and 80-60% in the other, and 0 otherwise. The participation grade will be added onto the final average with a possible 0.5 bonus at the end of the term, affecting all borderline grades. Late arrivals and early departure will be also noted.
Students are expected to maintain the highest standards of academic integrity. All work submitted must be original and properly cited. Plagiarism, cheating, or any form of academic dishonesty will result in immediate consequences as outlined in the university's academic integrity policy.
This is a Core IMPACTS course that is part of the STEM area
Core IMPACTS refers to the core curriculum, which provides students with essential knowledge in foundational academic areas. This course will help master course content, and support students’ broad academic and career goals.
This course should direct students toward a broad Orienting Question:
- How do I ask scientific questions or use data, mathematics or technology to understand the universe?
Completion of this course should enable students to meet the following Learning Outcomes:
- Students will use the scientific method and laboratory procedures or mathematical and computational methods to analyze data, solve problems and explain natural phenomena.
Course content, activities and exercises in this course should help students develop the following Career-Ready Competencies:
- Inquiry and Analysis
- Problem-Solving
- Teamwork
